In my last post, I explained the game theory mathematics of the standard game of Rock Paper Scissors (RPS), and what the Nash equilibrium is and how it works. Now I will show a similar analysis, but based on a variant of RPS where winning with rock gets you 1 point, winning with scissors gets you 2 points, and winning with paper gets you 3 points.
We can solve for the Nash equilibrium by doing a probability tree of all the different possible combinations, as before with the standard RPS. In instances where you win, add that many points. When you lose, subtract that many points (your opponent gaining points is equivalent to you losing points). As before, we will choose R, P, and S according to some random distribution, where \(R\) is our probability of choosing rock, \(P\) is our probability of choosing paper, and \(S\) is our probability of choosing scissor. Similarly we define the variables \(R’\), \(P’\), and \(S’\) to be the probabilities chosen by our opponent. Doing so, we get the following expected point gain each time the game is played:
\(g=0RR’ – 3RP’ + RS’ + 3PR’ + 0PP’ – 2PS’ – 1SR’ + 2SP’ + 0PP’\)
Remove the zero terms and then group them by \(R\)’, \(P’\), and \(S’\):
\((-3R + 2S)P’ + (R-2P)S’ + (3P-S)R’\)
For the equilibrium condition, we want the total to be 0, and we want it to be independent of whatever our opponent chooses for \(R’\), \(P’\), or \(S’\). We do that by saying that each of the terms in the parenthesis must be equal to 0. This gives us 3 equations:
\(\begin{matrix}
-3R + 2S = 0 \\
R – 2P = 0 \\
3P – S = 0
\end{matrix}\)
Solve the 3 equations for the 3 unknowns, and you get \(R = \frac{1}{3}\), \(S = \frac{1}{2}\), and \(P = \frac{1}{6}\). \(R+P+S = 1\) as it should. You can substitute these into the original equation and prove to yourself that no matter what your opponent chooses for \(R’\), \(P’\), and \(S’\), the expected return is always 0.
So… if you’re one of the 3 people on the entire internet that is still reading this thing, you may be asking yourself, “what about when my opponent doesn’t choose the Nash equilibrium? Is there an optimum \(R, P, S\) that will maximize my expected score?”
It turns out there is, and the answer is a quite simple, though getting there takes a bit of algebra. Take the formula for the expected point gain as before (terms equal to 0 eliminated):
\(-3RP’ + RS’ + 3PR’ – 2PS’ – 1SR’ + 2SP’\)
Use \(R+P+S=1\) and \(R’+P’+S’=1\) to eliminate \(S\) and \(S’\) so it’s only in terms of \(R\), \(P\), \(R’\), and \(P’\), and define this as a function \(g(R,P)\):
\(g(R,P) = -6RP’ + 2P’ + 6PR’ – 2P + R – R’\)
Now we have a surface function of two variables, \(R\) & \(P\), with \(R’\) and \(P’\) being constants. We can imagine this being in a 2D domain with R as the x-axis and P as the y-axis. So the domain in question will be a triangle with vertices at points \((1,0)\), which corresponds to \(R=1\) and \(P=S=0\). Similarly, \((0,1)\) corresponds to \(P=1\) and \(R=S=0\), and \((0,0)\) corresponds to \(S=1\) and \(R=P=0\).
We could then take the calculus approach and find the local maxima of \(g(R,P)\), but we really don’t have to do that. Looking at \(g(R,P)\), it is linear w.r.t. both \(R\) and \(P\), and so \(g(R,P)\) is a flat plane, tilted in some direction determined by \(R’\) and \(P’\). Also we know from calculating the Nash equilibrium that \(g\left(\frac{1}{3},\frac{1}{6}\right)=0\) (i.e. when we choose the Nash equilibrium that expected point gain \(g(R,P)=0\) ), and that when \(R’=\frac{1}{3}\) and \(P’=\frac{1}{6}\) that the plane will be coplanar with the X-Y plane [i.e. when our opponent chooses the Nash equilibrium then \(g(R,P)\) will always be zero no matter what we choose, that is only possible when the flat plane is zero everywhere].
Any deviation from those values by \(R’\) and \(P’\) will cause the plane to tilt in some direction. Since it is now tilting, there will be a direction that increases the value of \(g(R,P)\), and since \(g(R,P)\) has a constant slope everywhere, the maximum within the triangle-shaped domain must be on one of the points \((1,0)\), \((0,1)\), or \((0,0)\) [or perhaps two of the points will have the same maximum value].
So the optimal choice will either be \(R=1\) (with \(P=S=0\)), \(P=1\) (with \(R=S=0\)), or \(S=1\) (with \(R=P=0\)). Simply evaluating the first equation above for these three choices and seeing which one maximizes the expected point gain will give you your choice.
So for example, here is the surface for \(g(R,P)\) we get when our opponent chooses rock, paper, and scissors with equal frequency, or \((R’,P’,S’)=\left(\frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\). In our equation \(S’\) was eliminated, so for calculating \(g(R,P)\) we just need to say that \((R’,P’)=\left(\frac{1}{3},\frac{1}{3}\right)\):
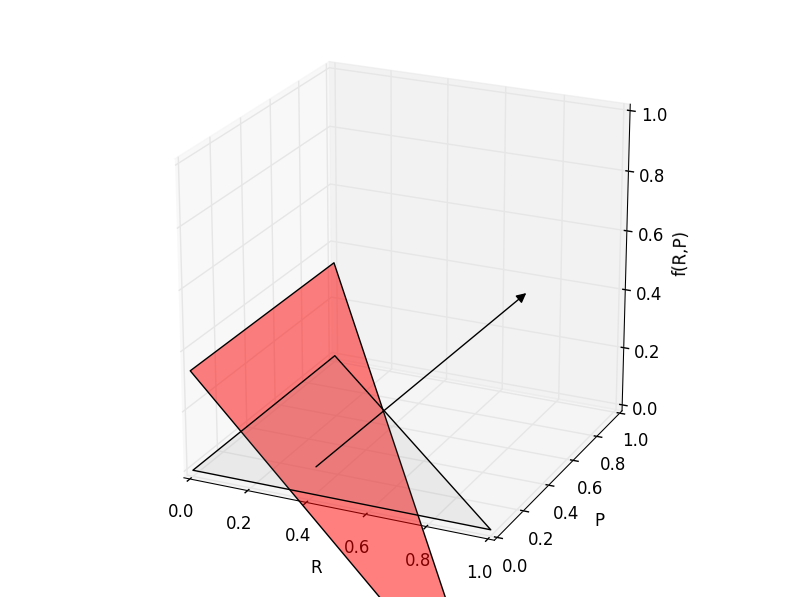
In this plot the gray triangle is the original domain in the previous image, the red triangle is the actual surface of \(g(R,P)\), and the black arrow is a normal vector from the plane coming from the Nash equilibrium point at \(g\left(\frac{1}{3},\frac{1}{6}\right)=0\).
It appears that the red triangle is tilted along the \(R=\frac{1}{3}\) line, so that both \((R,P)=(0,0)\) and \((R,P)=(0,1)\), or in other words playing scissors every time or paper every time (or some mix of the two) will give you the maximum expected point gain of \(\frac{1}{3}\) every time that you play.
Now what if our opponent chooses a strategy that is close to but not quite the Nash equilibrium? How much of a point gain can we expect by using the optimal strategy?
Here is the surface for \(g(R,P)\) if our opponent chooses \((R’,P’)=\left(\frac{1}{3}+0.01,\frac{1}{6}-0.01\right)\):
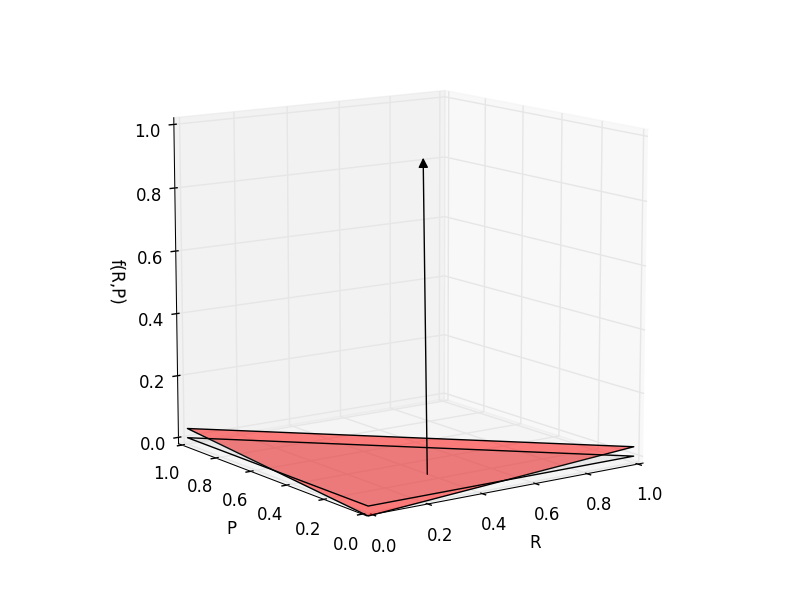
The slope of the response surface is much less, as reflected by the fact that our opponent’s choice of R,P, and S is much closer to the Nash equilibrium. In this case, it turns out that choosing either rock or paper every time will give the optimal point gain, in this case an expected point gain of only 0.03 each time we play.
Of course choosing rock or paper every time would be something that our opponent, if not a mindless robot, would be able to easily capitalize on. What if instead we only slightly perturb our choice of \((R,P)\) away from the Nash equilibrium like our opponent did, but instead perturb it in the direction that gives us the maximum expected point gain?
The distance we move from \((R,P)=\left(\frac{1}{3},\frac{1}{6}\right)\) is the same as our opponent. He moved 0.01 in the R-direction, and -0.01 in the P-direction, for a total distance of \(\frac{\sqrt{2}}{100}\). We know that playing rock or paper every time will maximize our expected score, this corresponds to the line \(P+R=1\). The shortest path to this line is to move perpendicular to it, which is the vector direction \((1,1)\). So this means we should choose the point \((R,P)=\left(\frac{1}{3}+0.01,\frac{1}{6}+0.01\right)\). If we do so, our expected point gain each time we play the game is \(g(R,P)=0.0012\).
My next question is then, how many games do we have to play in order to have, say, a 95% confidence that our score will be greater than our opponent? Remember that what we calculated above is the expected gain, which is kind of like taking a series of many, many games and taking the average. The outcome of any 1 game is random, but after many games we expect to pull ahead slightly. However I’m really rusty on this kind of math and I don’t remember how to do it. I’ll have to review a bit.
